VIDEOS

Grado de concentracion

Las medidas de forma permiten conocer que forma tiene la curva que representa la serie de datos de la muestra. En concreto, podemos estudiar las siguientes características de la curva:

a) Concentración: mide si los valores de la variable están más o menos uniformemente repartidos a lo largo de la muestra.

b) Asimetría: mide si la curva tiene una forma simétrica, es decir, si respecto al centro de la misma (centro de simetría) los segmentos de curva que quedan a derecha e izquierda son similares.

c) Curtosis: mide si los valores de la distribución están más o menos concentrados alrededor de los valores medios de la muestra.

a) Concentración

Para medir el nivel de concentración de una distribución de frecuencia se pueden utilizar distintos indicadores, entre ellos el Indice de Gini.

Este índice se calcula aplicando la siguiente fórmula:

IG =	S (pi - qi)
	----------------------------
	S pi
(i toma valores entre 1 y n-1)

En donde pi mide el porcentaje de individuos de la muestra que presentan un valor igual o inferior al dexi.

pi =	n1 + n2 + n3 + ... + ni
	----------------------------	x 100
	n

Mientras que qi se calcula aplicando la siguiente fórmula:

qi =	(X1*n1) + (X2*n2) + ... + (Xi*ni)
	-----------------------------------------------------	x 100
	(X1*n1) + (X2*n2) + ... + (Xn*nn)

El Indice Gini (IG) puede tomar valores entre 0 y 1:

IG = 0 : concentración mínima. La muestra está uniformemente repartida a lo largo de todo su rango.

IG = 1 : concentración máxima. Un sólo valor de la muestra acumula el 100% de los resultados.

Ejemplo: vamos a calcular el Indice Gini de una serie de datos con los sueldos de los empleados de una empresa (millones pesetas).

Sueldos	Empleados (Frecuencias absolutas)		Frecuencias relativas
(Millones)	Simple	Acumulada	Simple	Acumulada
x	x	x	x	x
3,5	10	10	25,0%	25,0%
4,5	12	22	30,0%	55,0%
6,0	8	30	20,0%	75,0%
8,0	5	35	12,5%	87,5%
10,0	3	38	7,5%	95,0%
15,0	1	39	2,5%	97,5%
20,0	1	40	2,5%	100,0%

Calculamos los valores que necesitamos para aplicar la fórmula del Indice de Gini:

Xi	ni	S ni	pi	Xi * ni	S Xi * ni	qi	pi - qi
x	x	x	x	x	x	x	x
3,5	10	10	25,0	35,0	35,0	13,6	10,83
4,5	12	22	55,0	54,0	89,0	34,6	18,97
6,0	8	30	75,0	48,0	147,0	57,2	19,53
8,0	5	35	87,5	40,0	187,0	72,8	15,84
10,0	3	38	95,0	30,0	217,0	84,4	11,19
15,0	1	39	97,5	15,0	232,0	90,3	7,62
25,0	1	40	100,0	25,0	257,0	100,0	0
x	x	x	x	x	x	x	x
S pi (entre 1 y n-1) =			435,0	x	S (pi - qi) (entre 1 y n-1 ) =		83,99

Por lo tanto:

IG = 83,99 / 435,0 = 0,19

Un Indice Gini de 0,19 indica que la muestra está bastante uniformemente repartida, es decir, su nivel de concentración no es excesivamente alto.

Ejemplo: Ahora vamos a analizar nuevamente la muestra anterior, pero considerando que hay más personal de la empresa que cobra el sueldo máximo, lo que conlleva mayor concentración de renta en unas pocas personas.

Sueldos	Empleados (Frecuencias absolutas)		Frecuencias relativas
(Millones)	Simple	Acumulada	Simple	Acumulada
x	x	x	x	x
3,5	10	10	25,0%	25,0%
4,5	10	20	25,0%	50,0%
6,0	8	28	20,0%	70,0%
8,0	5	33	12,5%	82,5%
10,0	3	36	7,5%	90,0%
15,0	0	36	0,0%	90,0%
20,0	4	40	10,0%	100,0%

En este caso obtendríamos los siguientes datos:

Xi	ni	S ni	pi	Xi * ni	S Xi * ni	qi	pi - qi
x	x	x	x	x	x	x	x
3,5	10	10	25,0	35	35	11,7	13,26
4,5	10	20	50,0	45	80	26,8	23,15
6,0	8	28	70,0	48	128	43,0	27,05
8,0	5	33	82,5	40	168	56,4	26,12
10,0	3	36	90,0	30	198	66,4	23,56
15,0	0	36	90,0	0	198	66,4	23,56
25,0	4	40	100,0	100	298	100,0	0,00
x	x	x	x	x	x	x	x
S pi (entre 1 y n-1) =			407,5	x	S (pi - qi) (entre 1 y n-1 ) =		136,69

El Indice Gini sería:

IG = 136,69 / 407,5 = 0,34

El Indice Gini se ha elevado considerablemente, reflejando la mayor concentración de rentas que hemos comentado.

Medidas de dispersion

1.- Rango: mide la amplitud de los valores de la muestra y se calcula por diferencia entre el valor más elevado y el valor más bajo.

2.- Varianza: Mide la distancia existente entre los valores de la serie y la media. Se calcula como sumatorio de las diferencias al cuadrado entre cada valor y la media, multiplicadas por el número de veces que se ha repetido cada valor. El sumatorio obtenido se divide por el tamaño de la muestra.

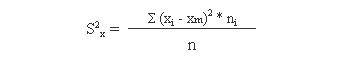
La varianza siempre será mayor que cero. Mientras más se aproxima a cero, más concentrados están los valores de la serie alrededor de la media. Por el contrario, mientras mayor sea la varianza, más dispersos están.

3.- Desviación típica: Se calcula como raíz cuadrada de la varianza.

4.- Coeficiente de varización de Pearson: se calcula como cociente entre la desviación típica y la media.

Ejemplo de medidas no centrales

Vamos a calcular los cuartiles de la serie de datos referidos a la estatura de un grupo de alumnos (lección 2ª). Los deciles y centiles se calculan de igual manera, aunque haría falta distribuciones con mayor número de datos.

Variable	Frecuencias absolutas		Frecuencias relativas
(Valor)	Simple	Acumulada	Simple	Acumulada
x	x	x	x	x
1,20	1	1	3,3%	3,3%
1,21	4	5	13,3%	16,6%
1,22	4	9	13,3%	30,0%
1,23	2	11	6,6%	36,6%
1,24	1	12	3,3%	40,0%
1,25	2	14	6,6%	46,6%
1,26	3	17	10,0%	56,6%
1,27	3	20	10,0%	66,6%
1,28	4	24	13,3%	80,0%
1,29	3	27	10,0%	90,0%
1,30	3	30	10,0%	100,0%

1º cuartil: es el valor 1,22 cm, ya que por debajo suya se situa el 25% de la frecuencia (tal como se puede ver en la columna de la frecuencia relativa acumulada).

2º cuartil: es el valor 1,26 cm, ya que entre este valor y el 1º cuartil se situa otro 25% de la frecuencia.

3º cuartil: es el valor 1,28 cm, ya que entre este valor y el 2º cuartil se sitúa otro 25% de la frecuencia. Además, por encima suya queda el restante 25% de la frecuencia.

Atención: cuando un cuartil recae en un valor que se ha repetido más de una vez (como ocurre en el ejemplo en los tres cuartiles) la medida de posición no central sería realmente una de las repeticiones.

Medidas de opocicion no central

Medidas de pocision central

Las medidas de posición nos facilitan información sobre la serie de datos que estamos analizando. Estas medidas permiten conocer diversas características de esta serie de datos.

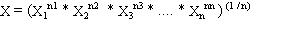
Las medidas de posición son de dos tipos:

a) Medidas de posición central: informan sobre los valores medios de la serie de datos.

b) Medidas de posición no centrales: informan de como se distribuye el resto de los valores de la serie.

a) Medidas de posición central

Las principales medidas de posición central son las siguientes:

1.- Media: es el valor medio ponderado de la serie de datos. Se pueden calcular diversos tipos de media, siendo las más utilizadas:

a) Media aritmética: se calcula multiplicando cada valor por el número de veces que se repite. La suma de todos estos productos se divide por el total de datos de la muestra:

Xm =	(X1 * n1) + (X2 * n2) + (X3 * n3) + .....+ (Xn-1 * nn-1) + (Xn * nn)
	---------------------------------------------------------------------------------------
	n

b) Media geométrica: se eleva cada valor al número de veces que se ha repetido. Se multiplican todo estos resultados y al producto final se le calcula la raíz "n" (siendo "n" el total de datos de la muestra).

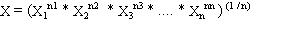
Según el tipo de datos que se analice será más apropiado utilizar la media aritmética o la media geométrica.

La media geométrica se suele utilizar en series de datos como tipos de interés anuales, inflación, etc., donde el valor de cada año tiene un efecto multiplicativo sobre el de los años anteriores. En todo caso, la media aritmética es la medida de posición central más utilizada.

Lo más positivo de la media es que en su cálculo se utilizan todos los valores de la serie, por lo que no se pierde ninguna información.

Sin embargo, presenta el problema de que su valor (tanto en el caso de la media aritmética como geométrica) se puede ver muy influido por valores extremos, que se aparten en exceso del resto de la serie. Estos valores anómalos podrían condicionar en gran medida el valor de la media, perdiendo ésta representatividad.

2.- Mediana: es el valor de la serie de datos que se sitúa justamente en el centro de la muestra (un 50% de valores son inferiores y otro 50% son superiores).

No presentan el problema de estar influido por los valores extremos, pero en cambio no utiliza en su cálculo toda la información de la serie de datos (no pondera cada valor por el número de veces que se ha repetido).

3.- Moda: es el valor que más se repite en la muestra.

Ejemplo: vamos a utilizar la tabla de distribución de frecuencias con los datos de la estatura de los alumnos que vimos en la lección 2ª.

Variable	Frecuencias absolutas		Frecuencias relativas
(Valor)	Simple	Acumulada	Simple	Acumulada
x	x	x	x	x
1,20	1	1	3,3%	3,3%
1,21	4	5	13,3%	16,6%
1,22	4	9	13,3%	30,0%
1,23	2	11	6,6%	36,6%
1,24	1	12	3,3%	40,0%
1,25	2	14	6,6%	46,6%
1,26	3	17	10,0%	56,6%
1,27	3	20	10,0%	66,6%
1,28	4	24	13,3%	80,0%
1,29	3	27	10,0%	90,0%
1,30	3	30	10,0%	100,0%

Vamos a calcular los valores de las distintas posiciones centrales:

1.- Media aritmética:

Xm =	(1,20*1) + (1,21*4) + (1,22 * 4) + (1,23 * 2) + ......... + (1,29 * 3) + (1,30 * 3)
	--------------------------------------------------------------------------------------------------
	30

Luego:

Xm =

1,253

Por lo tanto, la estatura media de este grupo de alumnos es de 1,253 cm.

2.- Media geométrica:

X =	((1,20^ 1) * (1,21^4) * (1,22^ 4) * .....* (1,29^3)* (1,30^3)) ^ (1/30)

Luego:

Xm =

1,253

En este ejemplo la media aritmética y la media geométrica coinciden, pero no tiene siempre por qué ser así.

3.- Mediana:

La mediana de esta muestra es 1,26 cm, ya que por debajo está el 50% de los valores y por arriba el otro 50%. Esto se puede ver al analizar la columna de frecuencias relativas acumuladas.

En este ejemplo, como el valor 1,26 se repite en 3 ocasiones, la media se situaría exactamente entre el primer y el segundo valor de este grupo, ya que entre estos dos valores se encuentra la división entre el 50% inferior y el 50% superior.

4.- Moda:

Hay 3 valores que se repiten en 4 ocasiones: el 1,21, el 1,22 y el 1,28, por lo tanto esta seria cuenta con 3 modas.

Distribucion de frecuencia agrupada

Supongamos que medimos la estatura de los habitantes de una vivienda y obtenemos los siguientes resultados (cm):

Habitante	Estatura	Habitante	Estatura	Habitante	Estatura
x	x	x	x	x	x
Habitante 1	1,15	Habitante 11	1,53	Habitante 21	1,21
Habitante 2	1,48	Habitante 12	1,16	Habitante 22	1,59
Habitante 3	1,57	Habitante 13	1,60	Habitante 23	1,86
Habitante 4	1,71	Habitante 14	1,81	Habitante 24	1,52
Habitante 5	1,92	Habitante 15	1,98	Habitante 25	1,48
Habitante 6	1,39	Habitante 16	1,20	Habitante 26	1,37
Habitante 7	1,40	Habitante 17	1,42	Habitante 27	1,16
Habitante 8	1,64	Habitante 18	1,45	Habitante 28	1,73
Habitante 9	1,77	Habitante 19	1,20	Habitante 29	1,62
Habitante 10	1,49	Habitante 20	1,98	Habitante 30	1,01

Si presentáramos esta información en una tabla de frecuencia obtendríamos una tabla de 30 líneas (una para cada valor), cada uno de ellos con una frecuencia absoluta de 1 y con una frecuencia relativa del 3,3%. Esta tabla nos aportaría escasa información

En lugar de ello, preferimos agrupar los datos por intervalos, con lo que la información queda más resumida (se pierde, por tanto, algo de información), pero es más manejable e informativa:

Estatura	Frecuencias absolutas		Frecuencias relativas
Cm	Simple	Acumulada	Simple	Acumulada
x	x	x	x	x
1,01 - 1,10	1	1	3,3%	3,3%
1,11 - 1,20	3	4	10,0%	13,3%
1,21 - 1,30	3	7	10,0%	23,3%
1,31 - 1,40	2	9	6,6%	30,0%
1,41 - 1,50	6	15	20,0%	50,0%
1,51 - 1,60	4	19	13,3%	63,3%
1,61 - 1,70	3	22	10,0%	73,3%
1,71 - 1,80	3	25	10,0%	83,3%
1,81 - 1,90	2	27	6,6%	90,0%
1,91 - 2,00	3	30	10,0%	100,0%

El número de tramos en los que se agrupa la información es una decisión que debe tomar el analista: la regla es que mientras más tramos se utilicen menos información se pierde, pero puede que menos representativa e informativa sea la tabla.

Distribución de frecuencias

La distribución de frecuencia es la representación estructurada, en forma de tabla, de toda la información que se ha recogido sobre la variable que se estudia.

Variable	Frecuencias absolutas		Frecuencias relativas
(Valor)	Simple	Acumulada	Simple	Acumulada
x	x	x	x	x
X1	n1	n1	f1 = n1 / n	f1
X2	n2	n1 + n2	f2 = n2 / n	f1 + f2
...	...	...	...	...
Xn-1	nn-1	n1 + n2 +..+ nn-1	fn-1 = nn-1 / n	f1 + f2 +..+fn-1
Xn	nn	S n	fn = nn / n	S f
Siendo X los distintos valores que puede tomar la variable.
Siendo n el número de veces que se repite cada valor.
Siendo f el porcentaje que la repetición de cada valor supone sobre el tota

• EJEMPLO

Medimos la altura de los niños de una clase y obtenemos los siguientes resultados (cm):

Alumno	Estatura	Alumno	Estatura	Alumno	Estatura
x	x	x	x	x	x
Alumno 1	1,25	Alumno 11	1,23	Alumno 21	1,21
Alumno 2	1,28	Alumno 12	1,26	Alumno 22	1,29
Alumno 3	1,27	Alumno 13	1,30	Alumno 23	1,26
Alumno 4	1,21	Alumno 14	1,21	Alumno 24	1,22
Alumno 5	1,22	Alumno 15	1,28	Alumno 25	1,28
Alumno 6	1,29	Alumno 16	1,30	Alumno 26	1,27
Alumno 7	1,30	Alumno 17	1,22	Alumno 27	1,26
Alumno 8	1,24	Alumno 18	1,25	Alumno 28	1,23
Alumno 9	1,27	Alumno 19	1,20	Alumno 29	1,22
Alumno 10	1,29	Alumno 20	1,28	Alumno 30	1,21

Si presentamos esta información estructurada obtendríamos la siguiente tabla de frecuencia:

Variable	Frecuencias absolutas		Frecuencias relativas
(Valor)	Simple	Acumulada	Simple	Acumulada
x	x	x	x	x
1,20	1	1	3,3%	3,3%
1,21	4	5	13,3%	16,6%
1,22	4	9	13,3%	30,0%
1,23	2	11	6,6%	36,6%
1,24	1	12	3,3%	40,0%
1,25	2	14	6,6%	46,6%
1,26	3	17	10,0%	56,6%
1,27	3	20	10,0%	66,6%
1,28	4	24	13,3%	80,0%
1,29	3	27	10,0%	90,0%
1,30	3	30	10,0%	100,0%

Si los valores que toma la variable son muy diversos y cada uno de ellos se repite muy pocas veces, entonces conviene agruparlos por intervalos, ya que de otra manera obtendríamos una tabla de frecuencia muy extensa que aportaría muy poco valor a efectos de síntesis